Phil Kreveld takes an in-depth look at variable speed drives ad what you need to know about them.

Variable speed drives are almost as common as bags of sugar. They are employed in all sorts of industries and domestic appliances, for example, air conditioners.

This article describes techniques used to improve the performance of AC drives, such as vector control, also called field orientation control (FOC), methods for extracting maximum motor voltage from the DC link voltages because we are dealing with inverter-based, variable speed drives, which derive their three phase voltages from a DC link, connected to line voltage via rectifiers.

We also look at regenerative and dynamic braking, motor drive cables and use of filters, bearing damage, vibration and cogging resulting from low speed operation. The motors of interest are three-phase induction motors, the workhorses of civilization.

Industrial variable speed drives fall into two basic categories: scalar control (control of torque via voltage and frequency) and vector control. The latter is the method of choice for loads requiring rapid variations in speed and torque and is the more complicated one.

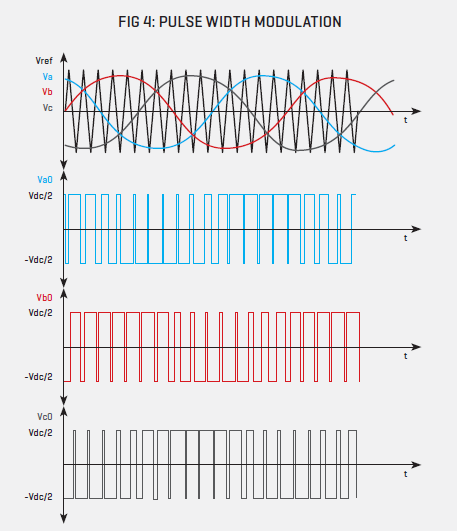
Scalar control works as follows: at low speed, motor winding impedances are low and high current flows, requiring voltage to be low—conversely, at high speed, impedances are high and voltage needs to be as well so that sufficient stator current is available for load torque. Scalar, volts per frequency (V/f) control is suitable for applications where speed-torque changes take place slowly. Scalar control generally uses an AC three-phase voltage generator to generate the inverter output via pulse width modulation (PWM) of its three-half bridge transistor switches (see fig 1).

Vector control drives often use space-vector modulation, which raises the question: what is a space vector. Think of an AC, three-phase motor. The stator phase windings are connected, each to their own phase, causing a rotating magnetic field—that magnetic field is an example of a space vector, and a similarly rotating voltage is also a space vector. Modulation methods are described further down.

Let’s get back to basics, so as to get a good grasp on control of induction motors. Torque is proportional to the square of applied voltage and the slip, i.e.: the difference between synchronous speed, (), where f is frequency and P, the number of poles of the stator.

The slip is the difference between synchronous speed and rotor speed as a fraction of synchronous speed. Therefore, starting torque for an induction motor is high because the rotor hasn’t as yet started revolving (slip is 1, i.e.: the synchronous speed for a 4 pole machine is 25 revs/sec at 50 Hz less rotor speed (0), at the start, divided by rotor speed).

The torque results from the induced rotor current magnetic field reacting with the stator’s synchronously revolving magnetic field. The rotor speeds up to a speed sufficiently lower to the synchronous speed in order to supply the load torque. Vector control is all about controlling the motor to provide the required torque at the desired speed. To cut to the chase, the rotor speed being less than the synchronous speed makes vector control trickier than for synchronous motors.

The principles of vector control in the inset, are based on synchronous motors, but make for a useful base to explain its application to induction motors.

On the left is a schematic representation of a DC motor with a separate field winding supply to that of the armature. The torque can be controlled by the field current and/or armature current. Because of the commutator, armature current physically always flows at right angles to the magnetic field, providing maximum torque available for a given field current/armature current (Fleming’s left-hand rule).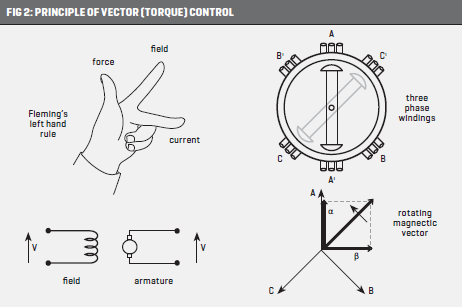

On the right, the cross section of a two-pole synchronous motor is shown. The magnetisation is due to the three-phase windings, sweeping around at the speed given by (), and reacts with the magnetic field of the rotor (permanent magnets are often used in electric vehicles or via slipring supplied DC current). Underneath the synchronous motor diagram, the space vectors of the three-phase windings are shown (the windings are spaced at 120° around the stator).

Applying three-phase voltages to the windings causes a rotating magnetic field (North-South magnetic vector), which can be resolved in two quadrature components, one y aligned with the magnet axis of the rotor (nominated the alpha (α) component), and the other at right angles (the beta (β) component). As is the case for the DC motor, it is the armature current field at right angles to the magnetisation direction that provides maximum torque.

The principle of vector control literally revolves around the control of torque. The β-α field components rotate, i.e. they are therefore AC quantities, and not very convenient to use in control loops. They are transformed to DC variables by using the motor shaft rotation (like placing an observer on the spinning rotor) to transform them into DC variables, ds (for direct) and dq (for quadrature). These latter, transformed variables control the synchronous motor; ds providing magnetisation intensity and dq the torque control.

Induction motors run below synchronous speed, making the transformation into ds and dq rotor components not directly available. One method of achieving this is by estimation of the slip and adding this to the angle described by the rotor, the latter being the integration over time of the shaft speed (this has to transformed by the number of poles of the motor to provide the equivalent of synchronous electrical angle). The diagram shown in fig 3 illustrates the principles of control.

Two modulation methods are used for variable voltage, variable frequency drives; pulse width modulation (PWM) and space vector modulation (SVM). In both cases a high frequency carrier wave (PWM) or switching frequency (SVM) are used to provide sufficient definition of motor voltage. PWM principles are illustrated in fig 4.

PWM modulation is suited to V/f control but not very well to the rapid changes in phase necessary for vector control for which SVM is ideal because it is a direct control of the magnetic flux vector.

Space vector modulation makes use of the three windings of a stator that constitute a pole pair (i.e. in a 2 pole motor, there three windings disposed at 120° to each other). Rather than emulating three, 120° separated sine wave voltages, the DC link voltage is switched rapidly in certain switching orders to the three phase windings and therefore setting up the magnetic flux space vector.

An example of a switch setting is shown below. The switches are IGBT transistors with freewheel diodes across them.

The DC link voltage across capacitor C causes current i_w to flow through field coil W and to return via coils U and V. The coil impedances are, of course, equal so that U and V in parallel are half the impedance of W. Therefore, the total impedance is equivalent to that of W (let’s call it 1) plus V and U in parallel, i.e. equal to ½, making the total impedance 3/2.

The current pulse comprising of 2/3  relative amplitude in W plus 1/3 in both V and U rise and fall at the same time interval but are displaced physically around the stator by 120°. They are shown in the space vector diagram below.

By means of switching arrangements (there are a total of 8 possibilities, including all windings connected to the positive terminal and all windings connected to the negative terminal, a rotating magnetic field vector is set up. Rather than using three sine waves for modulation as in the PWM mode, the α and β components are used to provide the basis for the switching arrangements.

For those interested in a ‘live’ demonstration there is an excellent YouTube presentation (https://www.youtube.com/watch?v=5x73LjZQ21o).

Unlike the control for synchronous motors which have the advantage of constant rotor flux by virtue of permanent magnets, or the equivalent via slip ring excitation, and therefore only need control of the quadrature component (β, dq), induction motors require the α and ds components, and therefore the magnitude of voltage is important.

The modulation index, i.e. the effective peak voltage as a ratio of the DC link voltage is less than 1.0 but can be built up by introducing a third harmonic in the phase voltages. This does not distort the line voltages to the motor because each line voltage is the difference of two phase voltages, and although 120° apart, the third harmonics are in phase, thus being cancelled.

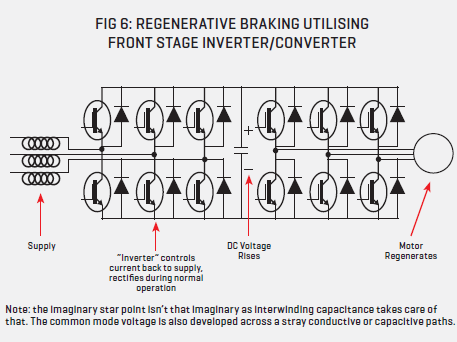
Regenerative braking of induction motors is an energy efficient procedure. By suddenly reducing the synchronous frequency of the stator winding, the mechanical load inertia will continue to spin the rotor, but at super synchronous speed, turning the motor into an induction generator, which, via the freewheel diodes of the inverter, will charge the DC link.

Provided the input is a switched IGBT power conversion stage rather than three rectifier half bridges, the excess DC link voltage can be fed back into the grid with the input stage operating as an inverter (refer to fig 5).

Dynamic braking also uses the motor in generating mode but now a chopper and braking resistor in the DC link absorb the excess energy.

If it weren’t for the electrical characteristics of the motor (leakage inductance and resistance of windings), the current drawn would be pulsed rather than a close to a smooth set of sinewaves — i.e. the motor acts a filter. However, the voltage waveforms are short rise-time pulses, travelling through the motor cable at speeds of 200 or so centimetres/microsecond. Switching frequencies as high as 15 kHz and voltage pulse rise times of 100 nanoseconds can stress both cable and motor insulation.

Depending on the characteristic impedance of the cable and that of the motor, reflections take place, and if of the same polarity as the arriving voltage pulses, a voltage ‘pile up’ occurs and this can cause motor insulation breakdown—and damage to the cable. The higher the carrier frequencies are, the more careful the selection of cable type and length has to be. The characteristic impedance of a cable has to be matched to that of the motor impedance—the high frequency motor impedance, if there is to be no voltage build-up.

So-called dV/dt filters can reduce the deleterious effect of low rise time voltage pulses on insulation but by virtue of phase shift, are not recommended for use in vector controlled drives. Long cable lengths should be avoided, in particular quarter wavelength equivalents which cause voltage standing waves, i.e, generally less than 30 metres.

Jerky motion (cogging) can occur at low speed and is due to magnetic field intensity build up at sharp edges on the rotor, or rotor displacement. Induction motors have the rotor slots disposed in a helical rather than cylindrical geometry to mainly avoid this. However, at the lower end of carrier frequencies in PWM drives, or switching frequency in SVM drives cogging can occur. For service at very low revs, a high carrier/switching frequency, typically 10 kHz drive is advisable.

Earth currents can damage motor bearings. In a wye-wired motor, or generally three-wire connection, there is no direct path to earth but as the diagram in fig 6 makes plain, capacitive earth current cannot be avoided. Stray conductive as well as capacitive paths to earth exist — it is only a matter of how much earth leakage there is.

Standard ELCB relays are not up to the task because of the presence of high frequency harmonics. Therefore, specialised relays should be considered such as microprocessor based relays suitable for DC components and higher frequency AC. Fluting in race ways of motor bearings is the result of earth current damage.