It might have been some time since you learned about voltage drop, so what are the requirements and the calculations? Chris Halliday explains.

The voltage in a circuit will drop due to the resistance and reactance of cables.

Designers and installers must consider voltage drop to ensure safety and proper operation of the equipment, ie: adequate voltage must be supplied.

If there is too much voltage drop the equipment won’t work, or safety will be compromised – such as a motor overheating and catching fire.

We therefore need to consider voltage drop before running cables and connecting loads. A larger cable than intended may be needed to ensure compliance with voltage drop requirements. Considering the voltage drop issue at the design stage of an installation will help avoid problems.

The Wiring Rules – AS/NZS30000, Section 2 at Clause 3.6 – provides the relevant detail for low-voltage installations. Clause 7.3 covers stand-alone systems and Clause 7.5.7 covers extra-low-voltage installations.

All sparkies should be familiar with these requirements.

Low voltage

Clause 3.6.1 discusses having the voltage for a piece of equipment higher than the lower limit of the Standard for that equipment.

The clause does allow for equipment not covered by a Standard to function safely at lower voltage, but it does not say this negates other sub-clauses in Section 3.6.

Conductors shall be sized to ensure that the voltage at any point in an installation does not drop more than 5% from the nominal (refer Clause 3.6.2). This equates to 11.5V for a 230V system and 20V for a 400V system.

The clause does not consider transient currents such as motor starting, solenoid closing and other similar applications.

The permissible voltage drop can be 7% if the supply comes from the low-voltage terminals of a substation on the premises and is dedicated to the installation (refer exceptions for Clause 3.6.2).

The voltage drop limits just mentioned are the total voltage drops for an installation. Voltage drops in the consumer mains, sub-mains and final sub-circuits must be tallied to ensure compliance with the limits.

Most of the voltage drop could be allocated to the final sub-circuit if there are no sub-mains and very short consumer mains. Likewise, long consumer mains and sub-mains will severely limit the available voltage drop in the final sub-circuit.

The old Australian Standards handbook HB301, for designing to the Wiring Rules, states that 2% to 3% is considered reasonable for the final sub-circuits, but it also discusses rearranging percentages for a satisfactory outcome.

Prudent placement of main switchboards and sub-boards will help to ensure that voltage drop is not an issue. This is a design matter and cannot be left to chance.

Stand-alone systems

Stand-alone systems, in accordance with Clause 7.3, are required to have a voltage drop of no less than 11% from the nominal.

This must take account of the output voltage of the source and the drop within the installation under normal operating conditions (refer exceptions for Clause 3.6.2).

It is really the same voltage-drop limit as for a grid-connected system, as the network company can have a drop of 6% and the installation a further 5%.

Extra-low voltage

A maximum voltage drop of 10% for extra-low-voltage installations, when conductors are carrying the circuit-operating current, is applied by Clause 7.5.7.

That is, unless the extra-low-voltage equipment (not exceeding 50V AC or 120V ripple-free DC) is specially designed to operate over a wider voltage range.

The 10% limit excludes transient currents caused by such things as motor starting, solenoid closing and other similar events.

Calculating voltage drop

Two methods are generally used for calculating voltage drop, as provided by AS/NZS3008.1.1, and both use a value of current in the calculation.

Clause 3.6.2 of AS/NZS3000 provides guidance on what value of current should be used in calculations and should not exceed:

• total circuit current;
• circuit maximum demand; or
• circuit protective device rating.

For circuits such as lighting and socket outlets, where the load is distributed over the circuit length, half the current rating of the protective device may be used for calculations (refer exceptions for Clause 3.6.2).

The first method uses conductor impedance, length and current for the calculation. This is slightly complex, as the resistance and reactance of the cable must be known to allow calculation of the cable impedance (refer Clause 4.3 of AS/NZS3008.1.1).

The resistance and reactance values for various cable types are provided by Tables 30-39 of AS/NZ3008.1.1. For smaller cables the reactance will have little effect on the total impedance and so can often be ignored.

Ohm’s law is used for this method as follows:

Vd = I x Zc

Where

Vd = voltage drop in volts

I = circuit current in amps

Zc = impedance of the circuit

Most sparkies will be more familiar with the second method:

Vd = (L x I x Vc)/1000

Where

Vd = voltage drop in volts

L = route length of the circuit in metres

I = circuit current in amps

Vc = cable voltage drop per ampere-metre length of circuit in millivolts per ampere-metre (mV/Am)

The value of Vc is provided by Tables 40-51 of AS/NZS3008.1.1.

The formula can also be rearranged to calculate Vc then look up a cable with a mV/Am value less than the value specified (not equal to, as there is no built-in margin for this simplified method).

Tables 40-51 are for three-phase circuits. Single-phase values of Vc require the three-phase values to be multiplied by 1.155. Don’t get caught by this little trap for young players.

The value of Vc is based on the maximum conductor temperature permitted by the cable insulation material. Allowance can be made if the cable operating temperature is considerably less than the maximum (refer Clause 4.4 of AS/NZS3008.1.1) and for differences in power factor.

The values of voltage drop calculated can be converted to a percentage by multiplying by 100 then dividing by 230 (for a 230V system).

The Wiring Rules has a simplified version of the latter method at Table C7. You simply need to multiply the length in metres by the current in amps and divide by the allowable voltage drop percentage, then find the size of cable with a value more than that provided by the Table C7.

Examples

A sparkie wants to connect a normal 16A single-phase power circuit using standard power cable – 2.5mm² twin and earth, PVC and PVC thermoplastic sheathed.

Voltage drop in the consumer mains and sub-mains has been calculated, and 3% is left of the allowable 5% for the circuit. The final socket outlet has a route length of 40m.

A 3% voltage drop = 0.03 x 230 = 6.9V (this value must not be exceeded).

The current for the calculations will be 8A, as the socket outlets will be distributed along the circuit (refer Clause 3.6.2 exception 1 of the Wiring Rules).

The impedance method:

The resistance of the cable is found by using Table 35 of AS/NZS3008.1.1 and the 75°C value, ie: 9.01Ω/km.

Vd = I Zc

= 8 x 9.01/1000 x 40 x 2 (don’t forget there are two conductors, the active and the neutral return).

= 5.8V. This value passes the 3%/6.9V voltage drop requirement set by the installation requirements.

The mV/Am method

The Vc value is found for the 2.5mm² cable using Table 42 of AS/NZS3008.1.1 and the 75°C value, ie: 15.6mV/Am

Vd = (L x I x Vc)/1000

= (40 x 8 x 15.6 x 1.155)/1000 (don’t forget the 1.155, as the mV/Am value in the table is for a three-phase circuit)

= 5.8V

Both methods align – we must know what we are doing! Again this passes the 3% requirement.

The simplified mV/Am method

Am/%V = (L x I)/%Vd

= (40 x 8)/3

= 106.7 Am/%V

Looking up Table C7 and selecting the cable with a value not less than 106.7 Am/%V, we find that 2.5mm² is the minimum size standard cable we can use for this project. So, we come up with the same result – it’s 2.5mm² cable.

Other considerations

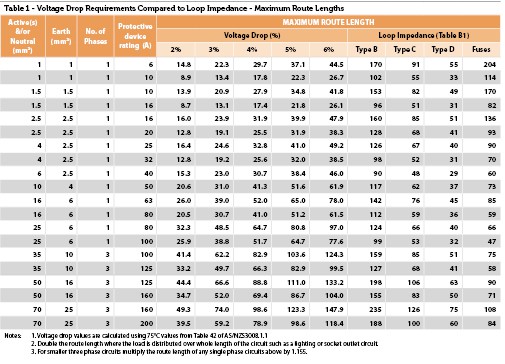
The Wiring Rules provides Table B1 for maximum route lengths for circuits based on loop impedance.

This does not consider voltage drop, so I have created Table 1 to compare maximum route lengths for loop impedance with voltage drop in the same circuits.

I have also created Table 2, which converts the values of loop impedance to voltage drop.

A comparison of both tables shows that, in most cases, voltage drop requirements are often more stringent than loop impedance requirements. Using loop impedance route lengths or impedance values in isolation is likely to result in non-compliance with the Wiring Rules for voltage drop.

Conclusion

Voltage drop must be considered when designing and installing electrical wiring.

Compliance with voltage drop requirements will be achieved mainly by installing a large enough cable.

Total voltage drop in a low-voltage installation is usually 5%. However, this can be 7% if the supply comes from the low-voltage terminals of a substation on the premises and is dedicated to the installation.

The allowable voltage drop must be split between the consumer mains, sub-mains and final sub-circuits to achieve an overall compliant outcome.

Maximum route lengths and fault loop impedance requirements do not generally ensure compliance with voltage drop rules.