Preventing power wastage can generate additional work, writes Bob Harper. Contractors should use the energy-awareness argument on existing and potential customers.

Many electricians have told me they don’t remember Ohm’s Law, and I live in hope that they are pulling my leg.

So what exactly does an electrician need to know about hysteresis? In this age of green energy we are all encouraged to be aware of wasted power, and how to combat it.

Mechanical losses aside, the electrician has three main culprits to contend with:

• resistive losses, of which most of trades people are aware (we hope);

• reactive losses through magnetic effects; and

• reactive losses through capacitive or dielectric effects.

Of these, resistive losses are the most common and of greatest concern, but they are generally best understood.

Capacitive effects are relatively unknown to electricians and usually of little concern, although high-speed switching circuits such as motor speed controllers may change that.

But first, a recap – without suggesting you have forgotten all your apprenticeship studies. What follows is summarised from the textbook I co-wrote, Electrical Principles for the Electrical Trades, extended to explain some issues for working electricians.

Magnetising force (H)

Magnetising force is the magneto-motive fire (MMF) required to magnetise a unit length of a magnetic path. The unit is expressed in ampere-turns per metre and the symbol is H.

Flux density (B)

Magnetic flux (?) refers to the total flux generated by a magnetic source. The unit for flux is the Weber (Wb).

In many instances it is more important to know the density of the flux rather than its total strength. Density refers to the quantity of flux per unit area, or Webers per square metre (Wbm² or Wb/m²) which is also called a Tesla (T).

Tesla is easier to say and remember but Webers per square metre is more descriptive.

You may also come across an older term for flux, the Gauss, or you may be asked to use a Gauss-meter. One Tesla is equal to 10,000 Gauss.

Magnetisation (B/H) curves

In non-magnetic materials the density of flux is not an issue, therefore flux (?) will vary directly as the MMF (IN). Flux density (B) will consequently be directly proportional to the magnetising force (H), therefore a graph of B against H will be a straight line.

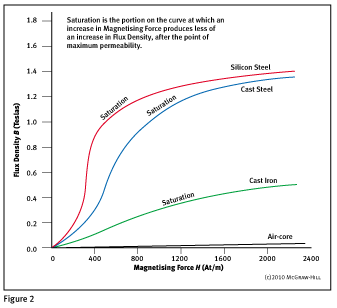
The B/H curve is used as an indicator of a magnetic material’s performance. These curves are commonly used as a means of comparing the magnetic characteristics of different types of magnetic materials and may be used to calculate the efficiency of a transformer or motor.

In magnetic circuits that have magnetic material in the core of the magnetism the B/H curves are no longer straight lines. When the value of H is low, small increases in the value of the magnetising force (H) will produce large increases in the value of flux density (B). This is due to the higher permeability of the magnetic material.

For higher values of H and B, increases in H will produce progressively smaller increases in B. As the magnetisation increases. a point is reached where large increases in H produce negligible increases in B.

Magnetic saturation is taking place, showing that magnetic materials are not linear – unlike resistors, for example.

In practice, it is not economical to magnetise steel to a flux density much beyond the point of magnetic saturation. A large increase in magnetising current produces only a small increase in flux density, resulting in a waste of electrical power without any useful increase in flux.

This also causes the saturation in transformers, which is a cause of harmonics and often of overheating.

Saturation is defined as occurring at a flux density near the centre of the ‘knee’ of the B/H curve as shown in Figure 1.

Permeability

The permeability of ferromagnetic materials therefore changes with differing values of flux density.

For a given flux density, permeability (?) is equal to the ratio B/H, which may be calculated directly from the B/H curve.

Note that permeability is akin to the resistivity of an electric circuit, and magnetic circuits have reluctance, which is like resistance in an electric circuit.

Magnetic hysteresis

So where does the energy go? Even after the magnetising force is removed, some magnetism remains.

This is a result of what is known as residual magnetism, that portion of the magnetic flux that remains in a ferromagnetic material when the magnetising force is removed. In other words, the material remains partly magnetised because it has some permanent magnetic properties.

In order to remove residual magnetism it is necessary to use a magnetising force – known as the coercive force – that acts in the opposite direction to the original magnetising force.

When a ferromagnetic material is magnetised first in one direction then in the other, it is necessary to use coercive force to overcome residual magnetism. The amount of coercive force required depends on the type of magnetic material.

The energy required for the coercive force is wasted and results in lower efficiency, causing heating of the magnetic core. That is where the ‘iron’ losses in a motor or transformer come from.

Hysteresis loops

If the magnetising force is plotted against the flux density in the classic B/H graph, this time showing both polarities of B and H, the hysteresis can be clearly seen.

Figure 3 shows the initial magnetisation curve OA. It begins at the origin (O) when no magnetic force or flux exists, and increases to the point A, which is well into the saturation region, or past the knee of the curve. The magnetising force (+H) results in a flux (+B) that is saturated.

As the magnetising force is reduced to zero, the flux density reduces as well, but not to zero. The part of the curve AB represents the removal of the magnetising force and resulting reduction in flux. Point B shows the flux density that remains, the residual flux (Br).

The coercive force (Hc) causes the flux density to be reduced to zero. Part BC of the curve shows the coercive force in effect.

The negative magnetising force now continues to increase to point D, which is the maximum negative magnetising force, and a point equal but opposite to point A on both axes.

Curve DEFA is an exact reflection of ABCD. Thus the combined magnetisation curves form a closed loop, ABCDEFA. This loop is commonly known as a hysteresis loop for a ferromagnetic material.

OB and OE indicate the values of residual flux density at zero magnetising force, and the value of the coercive force for removing that residual flux is indicated by OC and OFAL.

Hysteresis losses

Hysteresis loss appears in the form of heat in equipment magnetic cores. These are often iron, particularly in older equipment, hence the term ‘iron loss’.

Electrical power is consumed to make up for iron loss and it is usual to give values of iron loss for a particular material in watts per kilogram at a given frequency – eg: 50Hz.

How much energy is lost depends on the amount of coercive force required to reverse the magnetic dipoles in the material. This is directly proportional to the area within the hysteresis loop for that material per cycle. Remember that the hysteresis loss occurs every cycle.

The hysteresis loop determines the suitability of a magnetic material for a particular application.

In equipment that is subjected to a rapidly changing flux (ie: higher frequencies), it is important that the material used in the magnetic core has a hysteresis loop with a small area. Typically this means more exotic, and more expensive materials.

Permanent magnets should have a very large coercive force to be de-magnetised, and therefore the hysteresis loop should be very wide, with a large loop area.

Future trends

The electrical industry is changing due to an awareness of global warming and an energy crisis (or simply the need to save power), and the move toward new electronically commutated motors.

The energy crisis will bring more work for electrical contractors, as saving power will typically involve a refit and even a rewire. Savvy contractors should be using the energy-awareness argument to promote energy savings and create work opportunities.

Electronic motors, BLDC for example, that use electronics to gain greater performance and flexibility typically operate at higher frequencies. That therefore can create opportunities but also cause headaches for those that are still close to DC thinking.

The new Honda electric car motor has a cast-ceramic core and rotor, hollow shaft with directly mounted differential and final drive gears. Its electronic variable speed drive requires no gear changes over the whole range.

It recalls the way Fisher & Paykel did away with most of the mechanicals in its washing machines.